Gewichtete lineare Regression zur Kalibrierung

Hans-Joachim Kuss, Putzbrunn

In der Chromatographie erwartet man im Regelfall einen linearen Zusammenhang zwischen dem Messwert und der Konzentration. Dies muss natürlich verifiziert werden. Die beiden wichtigsten Detektoren in der Chromatographie, UV-Detektor in der HPLC und FID in der GC haben einen großen linearen Bereich. Massenspektrometer haben einen ausreichend großen linearen Bereich.

Sinnvollerweise wird man sich bei einer Chromatogrammserie immer mal wieder überzeugen, ob eine Leerprobe tatsächlich keine Veränderung der Basislinie an den Stellen zeigt, an denen bei Analysenproben Peaks erwartet werden. Das heißt, dass bei einer Konzentration von Null auch der Messwert Null sein und die lineare Kalibrierfunktion durch den Nullpunkt gehen muss.

Im Gegensatz dazu hat man bei der Messung der UV-Absorption in einer Küvette einen Messwert für die Untergrundabsorption. In der HPLC mit UV-Detektion wird diese Untergrundabsorption durch das Nullen (Autozero) des Detektors für alle Messwerte abgezogen. Ein chromatographisches Messsignal in einer Leerprobe an der Stelle des erwarteten Peaks kann nur als unzureichende Methode gewertet werden, was bedeutet, dass die Methode verbessert werden muss. Dies ist nicht zu verwechseln mit der stetigen Gefahr, eine zusätzliche interferierende Substanz unter dem Peak einer einzelnen Analysenprobe zu finden. Dagegen ist keine Methode vollständig gefeit.

Trotzdem wird in der chromatographischen Auswertung generell eine lineare Regression mit Achsenabschnitt durchgeführt. Dabei ist der Achsenabschnitt fast immer nicht signifikant. Auch aus statistischen Gründen muss dann der Achsenabschnitt auf Null gesetzt werden, weil sein Wert nur durch den Zufall bedingt ist.

Bei der Auswertung spielt ein nichtsignifikanter Achsenabschnitt nur dann eine Rolle, wenn der Arbeitsbereich groß ist. In diesem Fall kann ein (zufallsbedingter, d.h. nicht reproduzierbarer) Achsenabschnitt die kleinen Konzentrationen um mehr als 100% verfälschen. Ist der Achsenabschnitt signifikant, sollte ebenfalls an eine unzureichende Methode gedacht werden.

Die Regression wird auch Methode der kleinsten quadratischen Abweichungen genannt. Zur Kalibrierung wird eine lineare Funktion mit n (K=1 bis n; n=5 bis 10) Kalibrierpunkten verwendet, die durch eine sehr exakt bekannte Konzentration xK und ein mit einem Rauschen versehenen Messsignal yK beschrieben werden.

In der allgemeingültigen Form wird das Minimum für das Quadrat aus der Differenz des Messwerts yK und dem aus der Geradengleichung errechneten Messwert y(xK) errechnet, normiert auf die entsprechenden Varianzen, d.h. die x-Abweichungen werden als vernachlässigbar angesehen.

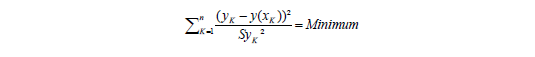
Um so rechnen zu können, muss die Standardabweichung Sy an jedem Kalibrierpunkt bekannt sein. Aus statistischer Sicht wäre es wünschenswert 10 Kalibrierpunkte 10-mal zu messen. Aus der Sicht des analytischen Chemikers wäre das ein unakzeptabel hoher Aufwand.

Zur Vereinfachung nimmt man an, dass die Standardabweichungen im Arbeitsbereich yK1 bis yKn gleich sind. Zur Absicherung macht man nur am untersten und obersten Kalibrierpunkt eine Mehrfachmessung und berechnet den F-Wert nach:

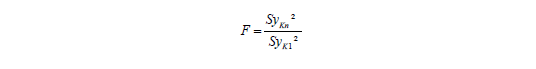
Findet man keinen signifikanten Unterschied, nimmt man an, dass obige Annahme gerechtfertigt ist und es können die Residuen R minimiert werden:

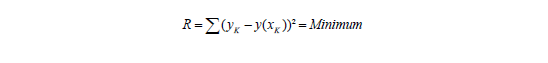
Die Residuen, d.h. der Abstand der gemessenen und berechneten Signalwerte sollten grundsätzlich in einem Residuenplot graphisch aufgetragen werden. Man kann daraus leicht die Homogenität der Abweichungen über den Konzentrationsbereich oder einen Trend erkennen, der evtl. auf eine quadratische Regressionsfunktion hinweist.

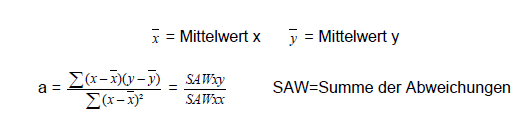
Die Bestgerade geht immer durch den Zentroid x und y. Ist a bekannt, lässt sich b berechnen:

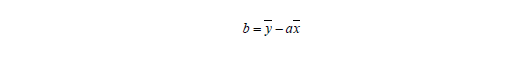
Aus der Varianz der y-Werte Sy² und der RSD lässt sich der Anteil der Varianz berechnen, der durch den Zusammenhang zwischen x- und y-Werten erklärt wird:

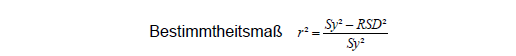
Besteht überhaupt keine Korrelation zwischen x und y, dann ist RSD=Sy und r²=0. Je stärker der Zusammenhang wird, desto kleiner wird RSD gegen Sy. Für RSD=0 ergibt sich ein vollständiger Zusammenhang mit r²=1 und dem Korrelationskoeffizienten r=1.

Sind a und b bekannt, lässt sich aus gemessenen Signalwerten die Konzentration einer Analysenprobe berechnen:

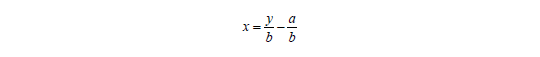
Die RSD ist eine Standardabweichung in y-Richtung. Sie kann analog zur Umrechnung von y- in x-Werte durch Division durch die Steigung in x-Richtung dargestellt werden. Damit erhält man die in den Validierungsrichtlinien genannte Verfahrensstandardabweichung. Diese dividiert man durch x, um den Verfahrensvariationskoeffizienten VVK zu erhalten:

Diese Kenngrößen sind nicht in den üblichen Statistikprogrammen enthalten, lassen sich aber in Excel einfach berechnen.

Die RSD ist die zentrale Größe zur Berechnung der Standardabweichung der Steigung und des Achsenabschnitts, der Nachweis- und der Bestimmungsgrenze sowie der Ergebnisunsicherheit U der errechneten Analysenwerte.

Leider findet sich in der Chromatographie bereits bei einem Arbeitsbereich von 10 oder größer häufig ein signifikanter F-Test. Das liegt daran, dass in der Chromatographie eher der Relativfehler konstant ist, als der Absolutfehler, wie bei der vereinfachten Regression angenommen, d.h.:

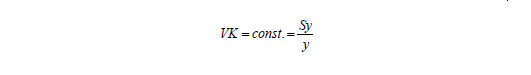
Bei einem konstanten Verhältnis zwischen Standardabweichung des Messwerts und dem Messwert selbst kann der Messwert als Schätzung der Standardabweichung benutzt werden. Damit wird obige Gleichung zu:

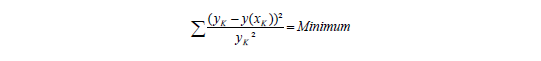
Dies ist nichts Anderes als die bekannte 1/y² Gewichtung der Varianzen, die bei den Integrationsprogrammen angewählt werden kann. Übliche weitere Gewichtungen sind 1/y, auch 1/x und 1/x² und auch 1/y½. Da ein Schätzwert für SDy gesucht wird, ist generell eine y-Gewichtung sinnvoller, als eine x-Gewichtung.

Den Fall gleicher Varianzen (Varianzenhomogenität; keine Gewichtung) könnte man „Apparatevarianz“ nennen. Dies wird angenähert der Fall sein, wenn wir nur eine einfache physikalische Messung durchführen. Die 1/y² Gewichtung, die auf einen konstanten VK im Messbereich zurückzuführen ist, könnte man „Volumenabhängige Varianz“ nennen. Dies beschreibt den Fall, wenn die Probenvorbereitung die Abweichungen dominiert. Die sehr wahrscheinlichen Volumenfehler müssen per se konzentrationsabhängig sein.

Nun sind alle Fälle zwischen diesen beiden Extremen einer Gewichtung w mit 1 (=keine Gewichtung) und einer 1/y² Gewichtung vorstellbar, die allgemein durch 1/yWE beschrieben werden können. Alle oben genannten y-Gewichtungen sind enthalten, aber zusätzlich ungeradzahlige Gewichtungen erlaubt. Der ungewichtete Fall ist durch den Wichtungsexponenten WE=0 beschrieben. Damit wird:

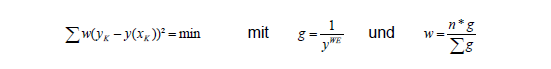
Das Problem besteht darin, WE aus den vorhandenen Daten möglichst sinnvoll abzuschätzen. Dies ist aus dem Varianzquotienten (F-Wert) unter Beachtung des y-Arbeitsbereichs nach folgender Gleichung möglich:

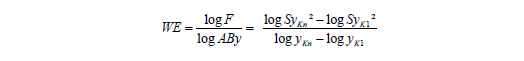
Dieses Verfahren könnte Varianzquotientengewichtung genannt werden.

Johnson, 1988, zeigt eines der wenigen Beispiele, bei denen Originalmessungen veröffentlicht wurden und bei dem Mehrfachmessungen für jeden Kalibrierpunkt vorliegen, so dass die jeweiligen Sy bekannt sind.

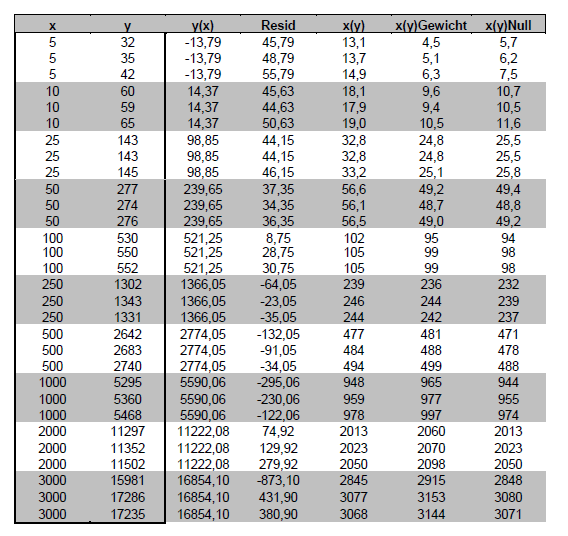
Die Originalwerte (peak height ratio response) in Spalte 2 wurden mit 1000 multipliziert, um sie leserlicher zu machen. Das beeinflusst die Rückrechnung in Konzentrationen nicht.

Die lineare Regression ohne Gewichtung ergibt die Geradengleichung y=5,63x-41,96, die graphisch plausibel aussieht – es fällt nur die große Variabilität des obersten Punktes auf. Anders sieht es aus, wenn man nur die ersten vier Kalibrierpunkte betrachtet, die man in der großen Graphik nicht mehr erkennen kann, die aber in der kleinen Graphik links oben deutlich zu sehen sind. Es ist offensichtlich, dass die unteren Kalibrierpunkte praktisch überhaupt nicht berücksichtigt werden. Dies zeigt auch die Abbildung der Residuen R=yK-y(xK) in der kleinen Graphik rechts unten. Die x(y)-Werte in Spalte 5 sind schon in der Arbeit von Johnsson enthalten, der eine 1/y-Gewichtung als Lösung des Problems vorschlägt.

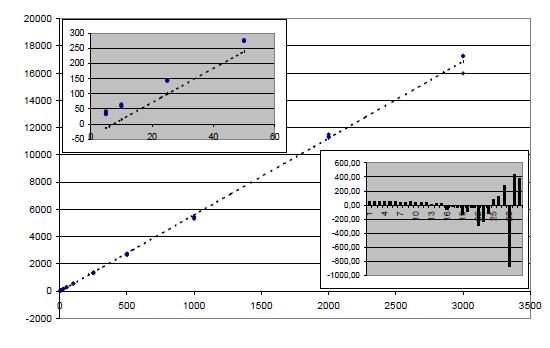
Jede Abweichung von der Geraden, d.h. jedes Residuum zieht die Gerade zu sich hin, sogar sehr stark, weil ja die Abweichungsquadrate aufsummiert werden. Wenn im unteren Teil der Gerade nur kleine Abweichungen auftreten, im oberen Teil nur große Abweichungen (inhomogene Varianzen, Heteroskedastizität), dann bleiben die unteren Punkte unberücksichtigt, weil sie kein Gewicht haben und die Gerade kann an ihnen zu weit vorbeigehen. Die Abweichungen bei den kleineren Konzentrationen haben die höhere Gewichtung „verdient“, weil sie (in Absoluteinheiten) erheblich genauer gemessen werden können.

Nehmen wir an, dass wir Messwerte hätten, die gerade den Kalibrierwerten entsprechen. Zur Zurückrechnung in Konzentrationen würde man graphisch einen Strahl in Höhe des Signals parallel zur x-Achse, d.h. durch die Messpunkte bis zur Geraden ziehen und von dort zur x-Achse, um die Konzentration abzulesen. Dadurch, dass die Gerade deutlich unterhalb der untersten Kalibrierpunkte verläuft und einen negativen, aber nicht signifikanten Achsenabschnitt hat, ergeben kleine Signalwerte viel zu hohe Konzentrationen.

Noch deutlicher zeigen dies die aus den Messwerten der Kalibrierkonzentrationen nach der Geradengleichung zurückgerechneten Konzentrationen in % des Soll-Konzentrationswertes.

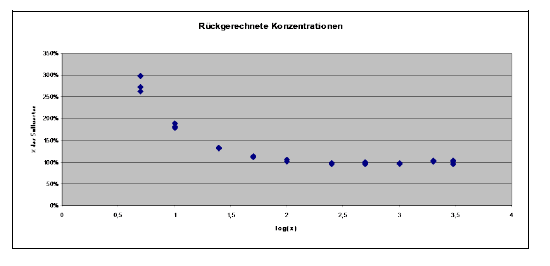
Die leichten negativen Abweichungen im mittleren oberen Konzentrationsbereich wiegen die großen relativen Abweichungen im unteren Konzentrationsbereich auf, weil sie als Absolutwert gleich sind. Es ist offensichtlich, dass die Abweichungen der niedrigsten Kalibrierkonzentrationen völlig unakzeptabel sind. Bei einem Messwert von Null errechnen sich bereits 7,5 ng/ml (=b/a). Diese Linearverschiebung beeinflusst die unteren Punkte viel mehr, als die oberen Punkte.

Der Wichtungsexponent errechnet sich nach obiger Gleichung zu 1,62. Dieser Wert wurde in eine entsprechende Excel-Tabelle eingesetzt:

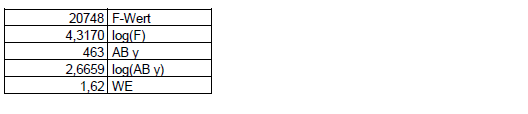
Die unteren 4 Kalibrierpunkte liegen mit Gewichtung fast exakt auf der Geraden. Es ergibt sich aus der Geradengleichung y=5,48x+7,25 ein positiver Achsenabschnitt, der 1,3 ng/ml entspricht. Die rückgerechneten Ergebnisse sind in der Spalte x(y)Gewicht dargestellt. Der Vergleich von x(y) und x(y)Gewicht zeigt, welche ungenügenden Ergebnisse die normale lineare Regression bringt. Mit der Nullpunktsgeraden weichen die Werte x(y)Null nur etwas mehr von den wahren Werten im unteren Konzentrationsbereich ab, als mit der Gewichtung.

Ein weiterer wesentlicher Grund, eine Gewichtung vorzunehmen, liegt in der adäquaten mathematischen Abbildung realistischer Messunsicherheiten U. Zu diesem Thema schrieb Doerffel 1990: „Deshalb muss die gewichtete Regression immer dann angewandt werden, wenn aus den Messungen Aussagen zur Präzision der Ergebnisse gefordert sind.“

Die bekannten Gleichungen zum Prognoseintervall PI (y-Abweichungen) und zur Messunsicherheit U (x-Abweichungen) verkomplizieren sich durch die Gewichtung nur geringfügig:

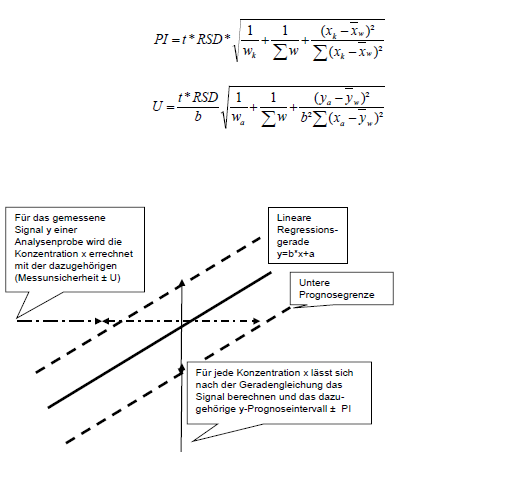
Beide Gleichungen ähneln sich sehr, weil U auf PI zurückgeführt wird. Die Unsicherheit der errechneten Konzentrationen resultiert aus der Unsicherheit der Messwerte. Graphisch wird dieselbe Grenzlinie einmal in y und einmal in x Richtung abgelesen.

Mit Gewichtung sind auch die unteren Konzentrationen im zulässigen Bereich der Messunsicherheit, wie die Abbildung demonstriert.

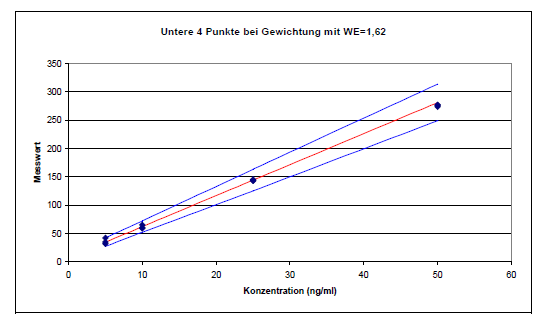
Insbesondere bei einem großen Arbeitsbereich macht man sich mit normaler linearer Regression durch eine letztlich falsche Rechnung (falls der F-Test signifikant ausfällt) die eigene meist mühsam optimierte Messung im unteren Konzentrationsbereich kaputt. Das schmerzt.